Text Section
To enter free text in your experiment, choose a Text paragraph section type.
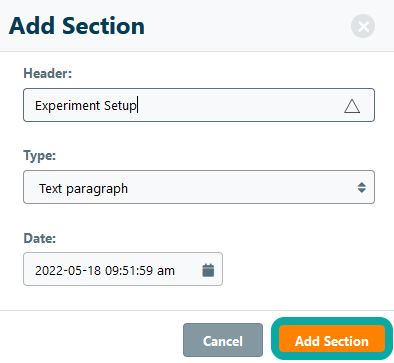
Once the section has been added, click on the Edit icon in the section header to open a text editor. An intuitive text editor will open that allows you to enter free text and offers the following basic functionality (find a more detailed description of all functionalities of the text editor here)
- Text formatting - bold, italic, underline, superscript and subscript
- Text import - import from Word with or without mark-up
- Text Styling - font type, size and color of text
- Lists - ordered and unordered list
- Alignment - text alignment left, right, centered, or justified
- Links - link other experiments or external sources
- Images - upload images and include them in text section (Please note that images saved in images sections cannot be downloaded separately and may have lower resolution)
- Symbols - symbols, special characters and Greek letters in lowercase and uppercase
- Mendeley Reference Manager - insert a link to Mendeley Reference Manager (only available if activated)
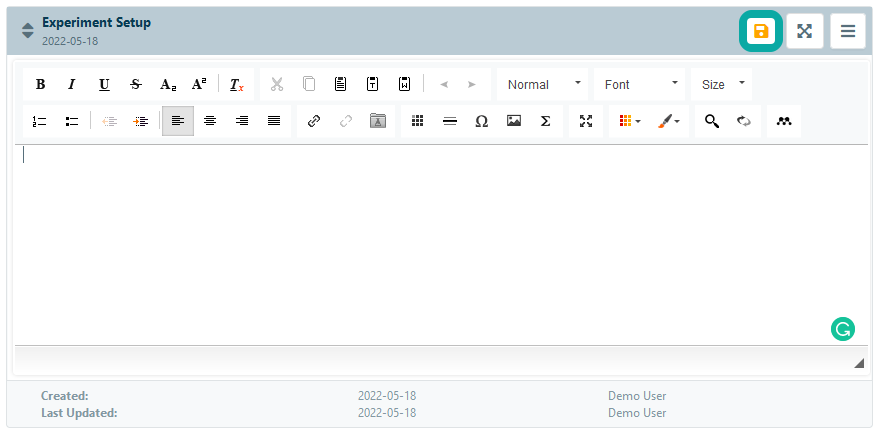
Enter the text and click the Save button to store the information in the ELN. A new version of the data will be stored, and the section footer will automatically be updated with the date and time of the most recent edit.
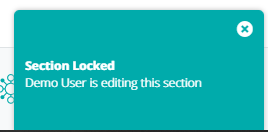
While a user is editing a section, the section becomes locked for other users to prevent collaborators from overwriting each others' data. When a user attempts to open a section that is being edited by another user, they receive the following notification:
Auto-save and Data recovery
While editing a text section, the content of a text section is automatically saved every 3 minutes. This enables users to recover any unsaved changes to a text section in the event that they do not save the section before navigating away from an experiment. The next time the user opens the text section, they will be given the option to restore unsaved changes.
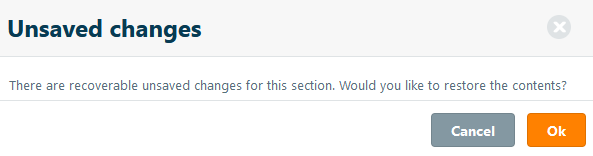
Click OK to open the unsaved changes in the text section. If you decide not to keep the unsaved changes, you can restore a previous version.
Autocorrect
Due to the data integrity and protection rules we have in place to protect the intellectual property of our clients, we are neither permitted nor willing to analyze our clients' data. Unfortunately, this also means that certain features which might be beneficial for our clients cannot be developed by us or installed. This includes auto-correction, as we would need to store and analyze the entries and data inputs of our clients and in a similar manner as companies like Google do with search entries.
Simply put: we would need to look at what our users are typing. Although we could try to analyze this information anonymously, it would still be theoretically possible to allocate users to specific entries, which would conflict with the provisions laid out in several data protection laws.